一、树的基本定义

Treedatastructure.png

图1.1 一颗树（图片来源：Wikipedia）

1、树基本概念

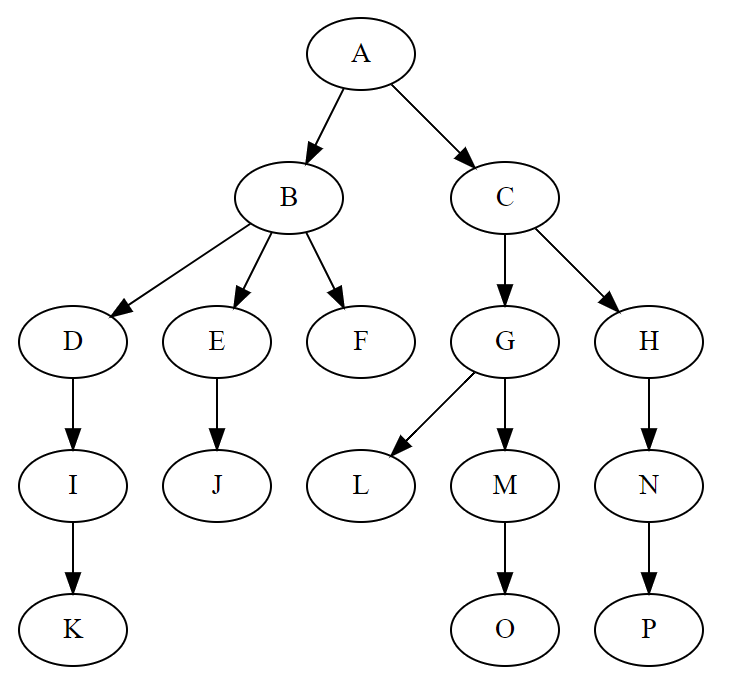
  1. 树：一种用来模拟拥有树状结构的数据结构模型，形似一颗倒置的树，是一种特殊的稀疏图
  2. 树的结点：每一个用于保存数据的元素，如图1.1中的A、B、C等
  3. 度：
    1. 节点的度：节点拥有的子元素的个数，例如图1.1中的B节点，度为3。
    2. 树的度：节点度最大的节点的度，如图1.1树的度为3
  4. 根节点：位于最顶端的节点，如图1.1中的A
  5. 叶子节点：度为0的节点，也成为末端节点，如图1.1中的K、J、L、O、P均为叶子节点
  6. 孩子节点：一个节点的子元素节点（节点子树的根节点），如图1.1中的B，孩子节点为D、E、F
  7. 双亲结点（父节点）：一个节点具有子元素节点，那么对于其所有子元素节点来说该节点为双亲结点（父节点），如图1.1中的D、E、F，他们的双亲节点为B
  8. 兄弟节点：具有相同双亲节点的节点称之为兄弟节点，如图1.1中的D、E、F，他们互为兄弟节点
  9. 祖先：由根节点到该节点之间的所有父节点，如图1.1，I节点的祖先节点为A、B、D
  10. 子孙：该节点子树的全部节点，如图1.1中B节点的子孙为D、E、F、I、J、K

2、深度与高度

  1. 深度指任意节点到根节点的唯一路径的距离，根节点深度为0。如图1.1，D节点深度为2。
  2. 高度指任意节点到叶子节点最长路径的距离，叶子节点高度为0。如图1.1 D节点的高度为
  3. 对于树来说，树的高度为根节点的高度，深度为叶子节点的深度的最大值，因此高度等于深度。如图1.1，深度与高度均为5
  4. 高度与深度的计算可使用递归，详见二叉树的高度与深度计算。

3、树的表示方法

  1. 双亲表示法：在树结构中，除根节点外所有节点均只有一个双亲节点，因此可以使用其双亲节点来表示该树。

    1. 存储方式

      数组下标 data parent
      0 A -1
      1 B 0
      2 C 0
      3 D 1
      4 E 1
      5 F 1
      6 G 2
      7 H 2
      8 I 3
      9 J 4
      10 K 8
      11 L 6
      12 M 6
      13 N 7
      14 O 12
      15 P 13

    2. 代码实现（Java）

      import java.util.Vector;

//树的节点
class TreeNode<T> {
  private T data;
  private int parent;
  public TreeNode(T data, int parent) {
      this.data = data;
      this.parent = parent;
  }
}

//树类
public class Tree<T> {
  private int countNodes;
  private Vector<TreeNode<T>> nodes;
  public Tree(int countNodes,Vector<TreeNode<T>> nodes){
      this.countNodes=countNodes;
      this.nodes=nodes;
  }
}

  2. 孩子表示法：将树中的每个节点与其子节点用链表形式连接起来，并将所有链表置入线性表中。

    1. 存储方式

      孩子表示法.png

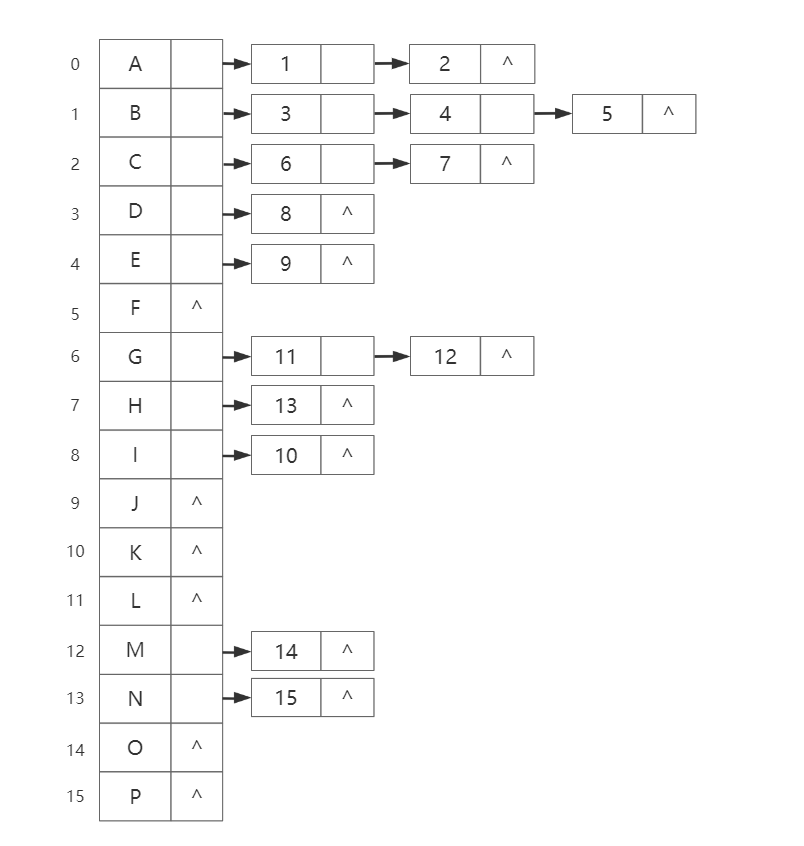
    2. 代码实现（Java）

  3. 孩子双亲表示法：同时采用孩子表示法和双亲表示法

    1. 存储方式

      孩子双亲表示法.png

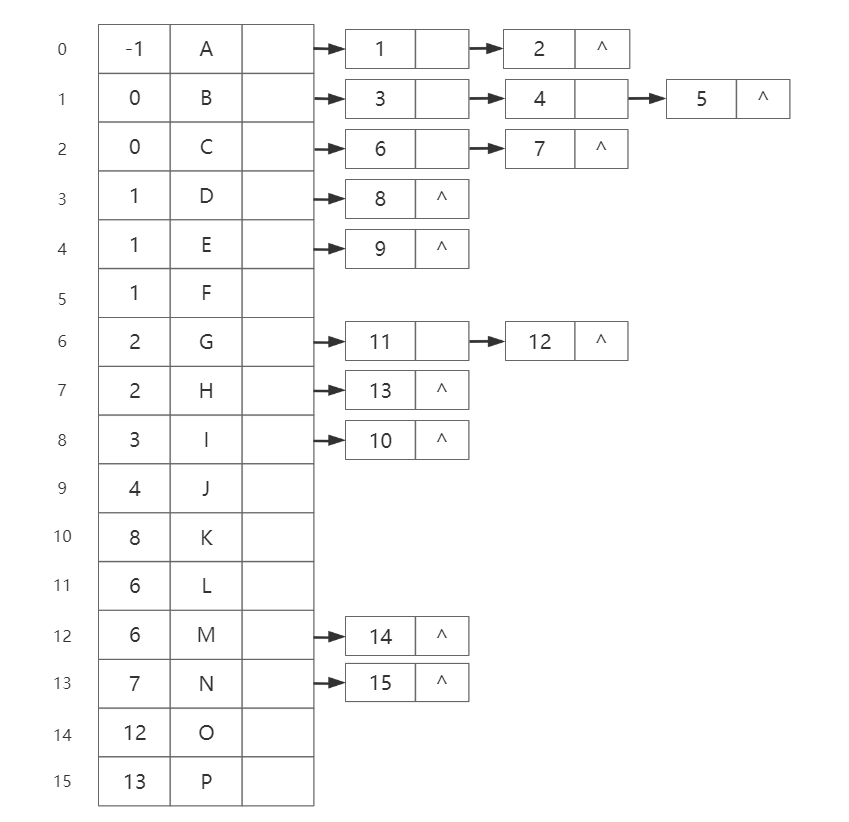
    2. 代码实现（Java）

  4. 孩子兄弟表示法

二、二叉树

1、二叉树的基本概念

  1. 二叉树
  2. 子树
  3. 斜树
  4. 满二叉树

2、二叉树的实现

3、二叉树的遍历

  1. 前序遍历
  2. 中序遍历
  3. 后序遍历
  4. 层序遍历

4、反转二叉树

三、树的遍历

1、深度优先搜索DFS

2、广度优先搜索BFS

四、特殊的树

1、红黑树

2、字典树

3、二叉排序树（二叉搜索树）

4、哈夫曼树

5、线索二叉树

6、平衡二叉树

7、堆

8、B树

9、B+树

本篇内容为原创内容，采用CC BY-NC-SA 4.0协议许可
2021-03-25 15:23
UtopiaXC
于大连

尽管如此，世界依旧美丽